Now we can easily generalize Tall's example about the role of microscopes (Tall, 1982,
2001). An infinitesimal increment ![]() of a differentiable function
of a differentiable function ![]() from its
point
from its
point ![]() can be written as follows
can be written as follows
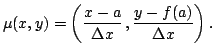
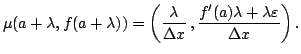
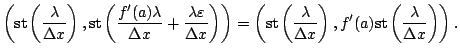
If ![]() is fixed, putting
is fixed, putting
![]() , we see that the points on the graph in
the field of view are mapped in the straight line
, we see that the points on the graph in
the field of view are mapped in the straight line
![]() , where
, where ![]() varies (see
Figure 2). Note that the slope of the line is, in effect, the derivative of
varies (see
Figure 2). Note that the slope of the line is, in effect, the derivative of
![]() in the point
in the point ![]() and the function is really indistinguishable from its tangent in an
infinitesimal neighborhood of
and the function is really indistinguishable from its tangent in an
infinitesimal neighborhood of ![]() .
.
In the following sections we will describe some interesting new mathematical situations in which such lenses can be used to construct a suitable mental representation.