The concept of tangent line of a real function is normally based on the standard
![]() concept of limit, which is intrinsically difficult to represent and not
immediately assimilable, for example, by students. We can avoid this trouble by
introducing a pictorial device that allows the visualization of small details in the
graph of a curve
concept of limit, which is intrinsically difficult to represent and not
immediately assimilable, for example, by students. We can avoid this trouble by
introducing a pictorial device that allows the visualization of small details in the
graph of a curve ![]() . This method was invented by Stroyan (1972) and improved by
Tall (1982, 2001): our intention is to continue and improve Tall's work by applying it to
many other different situations. We will work on the hyperreal number system
. This method was invented by Stroyan (1972) and improved by
Tall (1982, 2001): our intention is to continue and improve Tall's work by applying it to
many other different situations. We will work on the hyperreal number system
![]() and
will assume the non-standard analysis given by Abraham Robinson (1966).3
and
will assume the non-standard analysis given by Abraham Robinson (1966).3
In the present and in the following section we will explain the method and the classification proposed by Tall. In the last two sections we will introduce new types of diagrams called microscopes ``within'' microscopes and lenses ``within'' infinite telescopes.
By visualizing the difference between the numbers ![]() and
and
![]() (where
(where
![]() and
and
![]() is a positive infinitesimal), we can
introduce the map
is a positive infinitesimal), we can
introduce the map
![]() given by
given by
In general, for all
![]() , the function
, the function
![]() given by
given by
Given a ![]() -lens
-lens ![]() , proceeding by taking the standard part of
, proceeding by taking the standard part of ![]() , we obtain a
function from the field of view in
, we obtain a
function from the field of view in
![]() , called the optical
, called the optical ![]() -lens pointed in
-lens pointed in
![]() . The optical lenses are actually what we need to visualize infinitesimal
quantities. In fact, our eyes are able to distinguish clearly only images on the real
plane
. The optical lenses are actually what we need to visualize infinitesimal
quantities. In fact, our eyes are able to distinguish clearly only images on the real
plane
![]() . As such, the optical
. As such, the optical ![]() -lens translate on the
-lens translate on the
![]() plane, in favor of
our eyes, everything that differs from
plane, in favor of
our eyes, everything that differs from ![]() in the same order as
in the same order as ![]() . Higher order
details are ``too small'' to see and lower order details are ``too far'' to capture
within the field of view. Two points in the field of view that differ by a quantity of
higher order than
. Higher order
details are ``too small'' to see and lower order details are ``too far'' to capture
within the field of view. Two points in the field of view that differ by a quantity of
higher order than ![]() appear the same through the optical
appear the same through the optical ![]() -lens.
-lens.
This method also works in two coordinates (and, in general, in ![]() coordinates) by the application of a lens to every coordinate. The
map
coordinates) by the application of a lens to every coordinate. The
map
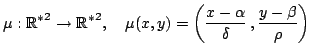
However, ![]() may not be infinitesimal. Depending on its nature,
there are different kinds of lenses: if
may not be infinitesimal. Depending on its nature,
there are different kinds of lenses: if ![]() is infinitesimal,
then the lens is called a microscope; if
is infinitesimal,
then the lens is called a microscope; if ![]() is finite
but not infinitesimal, then the lens is a window; if
is finite
but not infinitesimal, then the lens is a window; if ![]() is infinite, the lens is a macroscope. A window pointed at a
point with at least one infinite coordinate is called a telescope.
is infinite, the lens is a macroscope. A window pointed at a
point with at least one infinite coordinate is called a telescope.
Microscopes reveal infinitesimal details and telescopes allow us to visualize a structure at infinity. For example, through an optical microscope, a differentiable function looks like a straight line and through an optical telescope two asymptotic curves look identical.