

Next: Conclusion
Up: Perceiving the Infinite and
Previous: Microscopes ``within'' Microscopes
We now illustrate by way of example that asymptotic curves look
identical through an optical telescope.
The curves 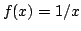 and
and 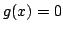 are asymptotic. Let
are asymptotic. Let  be a
positive infinite hyperinteger number and point a
be a
positive infinite hyperinteger number and point a 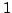 -lens in
-lens in
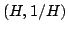 . We can see that
. We can see that
and by taking the standard parts, the optical
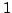 -lens maps
as
-lens maps
as 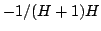 is infinitesimal. As such, a point in the form
is infinitesimal. As such, a point in the form
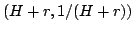 , where
, where
![$ r\in [0,1]$](img75.gif) , is mapped in the point
, is mapped in the point
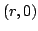 , and this means that
, and this means that 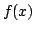 is indistinguishable from
is indistinguishable from
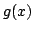 when
when 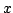 is infinite.
is infinite.
However, we can point an astigmatic lens ``within'' the telescope in 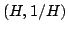 , in order
to visualize what really happens at infinity:
, in order
to visualize what really happens at infinity:
and, then, we obtain that a point on the hyperreal graph of 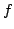 is mapped again as
follows
and the corresponding point of
is mapped again as
follows
and the corresponding point of 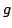
Figure 4:
The graph of 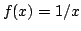 through an optical telescope.
through an optical telescope.
|
|
Hence, if we point a more powerful astigmatic lens within the
telescope, we can see that
the graphs of 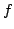 and
and 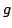 are straight, distinct, and parallel lines at infinity.
are straight, distinct, and parallel lines at infinity.


Next: Conclusion
Up: Perceiving the Infinite and
Previous: Microscopes ``within'' Microscopes
Riki
2002-09-01
![]() and
and ![]() are asymptotic. Let
are asymptotic. Let ![]() be a
positive infinite hyperinteger number and point a
be a
positive infinite hyperinteger number and point a ![]() -lens in
-lens in
![]() . We can see that
. We can see that
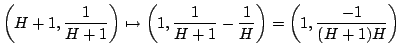
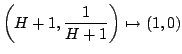
![]() , in order
to visualize what really happens at infinity:
, in order
to visualize what really happens at infinity:
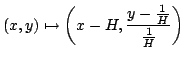
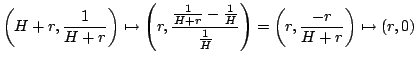
![]() and
and ![]() are straight, distinct, and parallel lines at infinity.
are straight, distinct, and parallel lines at infinity.